





Published on Apr 02, 2024
When it is only of interest to know the magnitude of the electrostatic force (and not its direction), it may be easiest to consider a scalar version of the law. The scalar form of the Coulomb’s Law relates the magnitude and sign of the electrostatic force F acting simultaneously on two point charges q1 and q2 as follows:
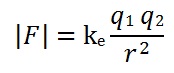
where r is the separation distance and ke is Coulomb’s constant. If the product q1q2 is positive, the force between the two charges is repulsive; if the product is negative, the force between them is attractive.
To estimate the charge induced on each one of the two identical styro foam balls (or pith balls) suspended in a vertical plane by making use of Coulomb’s law:-
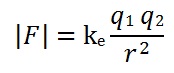
The fundamental concept in electrostatics is electrical charge. We are all familiar with the fact that rubbing two materials together - for example, a rubber comb on cat fur - produces a “static” charge. This process is called charging by friction.
The charged particles which make up the universe come in three kinds: positive, negative, and neutral. Neutral particles do not interact with electrical forces. Charged particles exert electrical and magnetic forces on one another, but if the charges are stationary, the mutual force is very simple in form and is given by Coulomb’s Law:
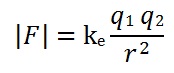
where F is the electrical force between any two stationary charged particles with charges q1 and q2(measured in coulombs), r is the separation between the charges (measured in meters), and k is a constant of nature (equal to 9x109 Nm2/C2 in SI units).
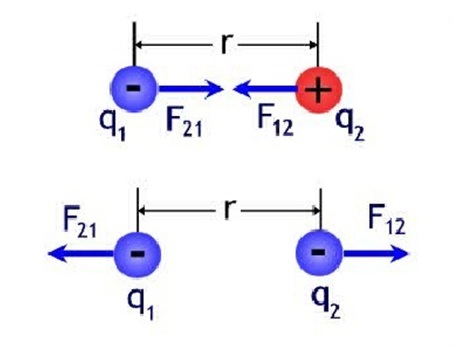
The study of the Coulomb forces among arrangements of stationary charged particles is called electrostatics. Coulomb’s Law describes three properties of the electrical force:
1)The force is inversely proportional to the square of the distance between the charges, and is directed along the straight line that connects their centres.
2)The force is proportional to the product of the magnitude of the charges.
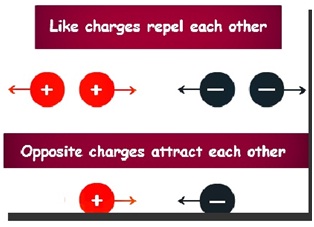
3)Two particles of the same charge exert a repulsive force on each other, and two particles of opposite charge exert an attractive force on each other.
Most of the common objects we deal with in the macroscopic (human-sized) world are electrically neutral. They are composed of atoms that consist of negatively charged electrons moving in quantum motion around a positively charged nucleus. The total negative charge of the electrons is normally exactly equal to the total positive charge of the nuclei, so the atoms (and therefore the entire object) have no net electrical charge. When we charge a material by friction, we are transferring some of the electrons from one material to another.
Materials such as metals are conductors. Each metal atom contributes one or two electrons that can move relatively freely through the material. A conductor will carry an electrical current. Other materials such as glass are insulators. Their electrons are bound tightly and cannot move. Charge sticks on an insulator, but does not move freely through it.
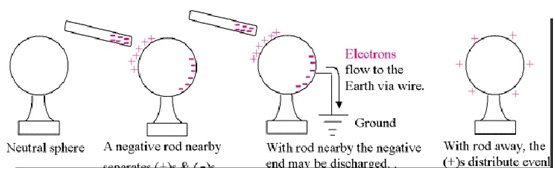
A neutral particle is not affected by electrical forces. Nevertheless, a charged object will attract a neutral macroscopic object by the process of electrical polarisation. For example, if a negatively charged rod is brought close to an isolated, neutral insulator, the electrons in the atoms of the insulator will be pushed slightly away from the negative rod, and the positivenuclei will be attracted slightly toward the negative rod. We say that the rod has induced polarisation in the insulator, but its net charge is still zero.
The polarisation of charge in the insulator is small, but now it’s positive charge is a bit closer to the negative rod, and its negative charge is a bit farther away. Thus, the positive charge is attracted to the rod more strongly than the negative charge is repelled, and there is an overall net attraction. If the negative rod is brought near an isolated, neutral conductor, the conductor will also be polarised. In the conductor, electrons are free to move through the material, and some of them are repelled over to the opposite surface of the conductor, leaving the surface near the negative rod with a net positive charge. The conductor has been polarised, and will now be attracted to the charged rod. Now if we connect a conducting wire or any other conducting material from the polarised conductor to the ground, we provide a “path” through which the electrons can move. Electrons will actually move along this path to the ground. If the wire or path is subsequently disconnected, the conductor as a whole is left with a net positive charge. The conductor has been charged without actually being touched with the charged rod, and its charge is opposite that of the rod. This procedure is called charging by induction.
• Small size identical balls (pitch or soft plastic)
• Physical balance or electrical balance
• Half meter scale
• Cotton thread
• Small stand
• Glass rod
• Silk cloth
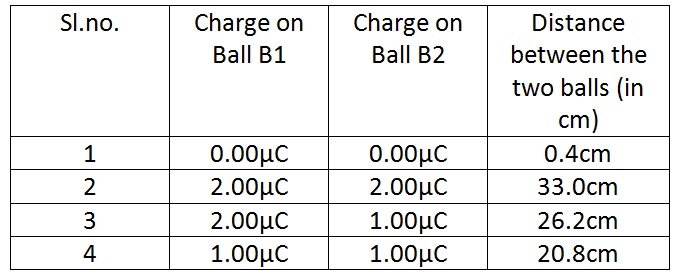
1. Measure the mass (m) of each of the two identical pith balls using a physical balance. 2. Hang the two balls from a rigid support using light silk or cotton threads of same length ‘l’.
3. Rub the glass tod silk cloth to induce charge on it. Now touch the glass rod with both the pith balls together so that equal charge is induced on both the balls.
4. When left freely, the two balls will repel each other. Measure the distance between the balls when are at rest. Note down the distance.
5. To change the charge on ball, take third uncharged ball touch it to any one of the two balls and take the third ball away, and repeat step 4.
6. Take other uncharged suspended with other uncharged 4th ball and take the 4th ball away and repeat step 4.
Mass of the pith balls m= 200 gm.
Radius of the ball a = 0.2 cm.
Length of thread l = 100 cm.
Let the force between two stationary charges be F.
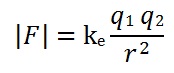
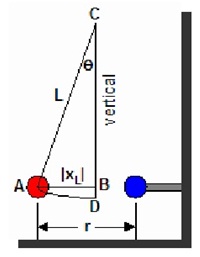
The weight of the ball w = mg
The restoring force on each ball = mg sinθ
From the diagram in the right in triangle ABC
Sinθ = x/2l
Let the charge on each ball be q1, q2 and q3 then at equilibrium
mg sinθ = (kq×q )/x2
Charge on the pith ball =√((mgr3)/2kl)
iCBSE.com
Wikipedia
Chemmicalland.com
Books.google.co.in
Physics NCERT class 12 book