To Measure the Speed of Sound at Room Temperature

Published on Apr 02, 2024

Abstract

In physics, sound is a vibration that typically propagates as an audible wave of pressure, through a transmission medium such as a gas, liquid or solid.

In human physiology and psychology, sound is the reception of such waves and their perception by the brain.[1] Humans can only hear sound waves as distinct pitches when the frequency lies between about 20 Hz and 20 kHz. Sound waves above 20 kHz are known as ultrasound and is not perceptible by humans. Sound waves below 20 Hz are known as infrasound. Different animal species have varying hearing ranges.

Sound is defined as "

(a) Oscillation in pressure, stress, particle displacement, particle velocity, etc., propagated in a medium with internal forces (e.g., elastic or viscous), or the superposition of such propagated oscillation.

(b) Auditory sensation evoked by the oscillation

Objective

The objective is to measure the speed of sound at Room Temperature.

Theory

Sound is a longitudinal wave that travels at a speed of v = 331m/s at STP conditions. A longitudinal wave is one that oscillates parallel to its propagation direction. The way an induced disturbance travels in a slinky is a longitudinal wave motion. At a frequency f that we speak or sing (Audio range: 200Hz - 2000 Hz), the wavelength λ of a sound wave is in the range of 150cm - 15cm. This may be verified by using the wave speed formula:

v = f λ

Resonance of Sound Waves in Open and Closed Pipes:

In music, a pipe open at both ends is called an open pipe, and a pipe open at one end only forms a closed pipe as shown below:

Sound

Maximum deviation of a wave from equilibrium position is called the "amplitude." For the motion (oscillations) of a sound wave in a pipe, when maximum deviation occurs at an open end, the sound amplifies. If a pipe has the right length, this happens and is associated with an intensified loudness confirming a resonance state. The repeatedly generated waves by a source (such as a tuning fork) keep combining constructively with reflected waves to form resonance. This is because of the fact that at an open end, air molecules are free to oscillate back and forth. At a closed end, air molecules are not free to perform wide oscillations. In other words, a closed end always forms a node and an open end can form an anti-node if the pipe's length is right.

The following figures show how the maximum and minimum of oscillations occur at open and closed ends for a certain wavelength at different pipe lengths:

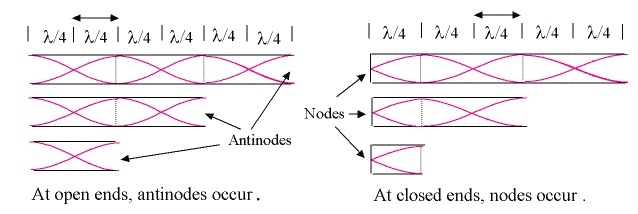
Speed of Sound

Note that, for simplicity, representation of transverse waves are used to show states of maximum and minimum oscillation at open and closed ends. Sound waves; however, are longitudinal and oscillate back and forth parallel to the pipe's length and not up and down as shown. These figures only indicate where maxima and minima occur for resonance to be heard.

As can be seen from the above figures, the length of a pipe must be a multiple of λ/4 for an anti-node (maximum) to occur at its open end.

For an open pipe (left figure), if the pipe's length is an even multiple of λ/4, each open end forms an anti-node and resonance occurs.

For a closed pipe (right figure), when the pipe's length is an odd multiple of λ/4, resonance occurs.

In this experiment, a closed pipe will be used. It will be seen that when the length of the pipe is an odd multiple of a certain length, the pipe is in resonance and intensified sound is heard.

At this point, it is suitable to repeat the definitions of wavelength and frequency.

Wavelength: Wavelength, λ , is defined as the distance from one peak to the next one on a wave. Of course, in general, wavelength is the distance between two successive points on a wave that are in the same state of oscillation.

Frequency: Frequency f is the number of waves (full λs) generated per second.

Speed of Sound

Materials Required:

A few tuning forks, a mallet, a resonance tube apparatus, and a calculator

Procedure:

1) Obtain a resonance tube apparatus. The apparatus is just a long piston-cylinder system that is used to make a variable length closed pipe, as shown:

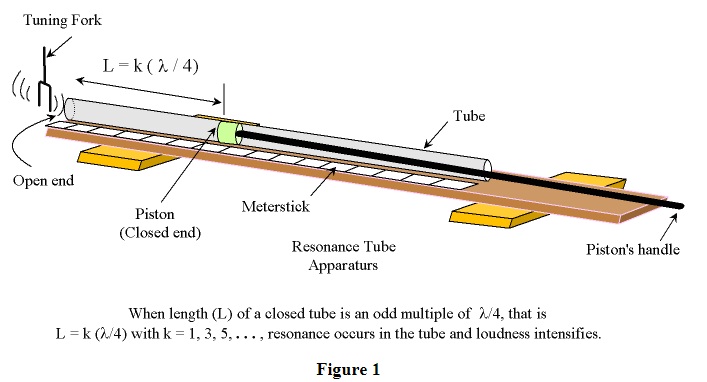
resonance tube apparatus

2) Hit a tuning fork of known frequency with a mallet to make it oscillate. This should be done away from the tube's opening so that it doesn't hit the glass tube causing it to break. While one group member is holding the oscillating tuning fork at about 1/2 to 1 inch from the pipe's opening, another member may pull the piston's handle out and increase the pipe's length until resonance is heard. A few trials and adjustments may be needed to locate the best length of the pipe at which the loudest possible sound can be heard.

3) Read the pipes length from the meter-stick and record it as L1.

Note that L1 = 1λ/4.

4) In a similar manner locate the position of the 2nd resonance. As you know the second resonance should occur at L2 = 3λ/4.

5) Calculate the wavelength λ as described below:

L1 = 1λ/4 and L2 = 3λ/4.

L2 - L1 = 3λ/4 - 1λ/4 = λ/2 or, λ = 2(L2 - L1). (1) Verify.

For your Information:

Note that λ can be calculated from either of L1 or L2 alone. As a rule of thumb, 0.6D must be subtracted from L1 if only L1 is used to solve for λ where D is the inner diameter of the pipe.

The same is true for L2. 0.6D must be subtracted from L2 if only L2 is used to calculate the λ from.

Now, it is better to use both L1 & L2 and subtract one from the other. In subtracting, the 0.6D correction of one cancels the 0.6D correction of the other and we don't have to deal with such correction at all; thus, just use Eqn. 1 above.

6) Once λ is determined, equation v = f λ may be used to find the measured value of v. Of course, f is the frequency of the tuning fork.

7) For accepted value, the empirical formula v(T) = [331 + 0.6T ]m/s may be utilized. In this equation, T is the ambient temperature in oC. Read the temperature from the thermometer in the room where the experiment is being performed.

8) Repeat the above steps for two other tuning forks of different frequencies.

9) Record all data in Table 1.