





Published on Feb 14, 2025
Prolonged, intensive exposure to hand-transmitted vibration could cause a series of disorders in the sensorineural, vascular, and muscular systems of the fingers, which are the major components of hand-arm vibration syndrome. The hand–arm responses to vibration have been mostly investigated in terms of biodynamic responses, which are believed to serve as the essential foundation for understanding the mechanisms associated with vibration-induced disorders and for developing better risk assessment methods. Moreover, thorough characterizations of the biodynamic responses are considered vital for design and assessment of vibration attenuation devices, and for developing hand–arm vibration simulators for assessment of power tools.
The vibration power absorption density (VPAD) is a good measure for the vibration exposure intensity of the soft tissues of the fingers. In order to calculate the VPAD at a fingertip, we proposed a hybrid modeling approach, which combines a 2D finite element (FE) model with a lumped parameter model. Whereas the lumped components are used to represent the global biodynamic characteristics of the hand-arm system, the FE component is used to predict the detailed stresses, strains, and VPAD in the fingertip The transmission of handle vibration to the wrist, elbow and the shoulder of the human hand and arm are characterized in the laboratory for the bent-arm and extended arm postures. Anti-vibration (AV) gloves have been increasingly used to help reduce the vibration exposure.
However, the exact mechanisms of the AV gloves have not been seriously analyzed and sufficiently understood. How to appropriately assess the effectiveness of AV gloves for protecting the hand remains an issue for further studies. Therefore, the vibration transmissibility of the glove, the ratio of the vibration at the glove- hand interface to the handle vibration, is typically used as a measure of the glove effectiveness .The proposed model is applied to predict the effectiveness of the glove in terms of vibration transmitted to the fingers-glove and palm-glove interfaces, the finger bones, and the wrist.
Vibration is the study of motions which repeat itself after an interval of time. It is the most important criteria that have to be considered during design. It is both useful and harmful to engineering systems. Unwanted vibrations may cause rapid wearing of machine parts, excessive stresses etc. Usually in industries, the workers dealing with powered hand tools. Clinical studies have shown that the operators of hand-held power tools are prone to develop various vibration induced disorders of the hand and arm, which are collectively referred as “Hand-Arm Vibration Syndrome (HAVS)”. Prolonged, intensive exposure to hand transmitted vibrations has been associated with a series of disorders in the vascular, sensorineural, musculoskeletal structures of the human fingers and hand-arm system.
The characteristics of HAVS, generated by the operation of power tools are considered to be affected by dynamics of coupled tool hand system. Hence the vibration transmission characteristics of power tools and proper vibration attenuation mechanism have to be investigated. The primary objective of the seminar is to analyze the vibration transmissibility in the finger tip[1], hand-arm system under different postures [2]. The primary technique used in study is “Vibration Power Absorption Density (VPAD)” technique. As a mean to eliminate vibration induced disorders, an anti-vibration glove [3] is analyzed. Mechanical equivalent models of finger tip and hand-arm system with glove are developed.
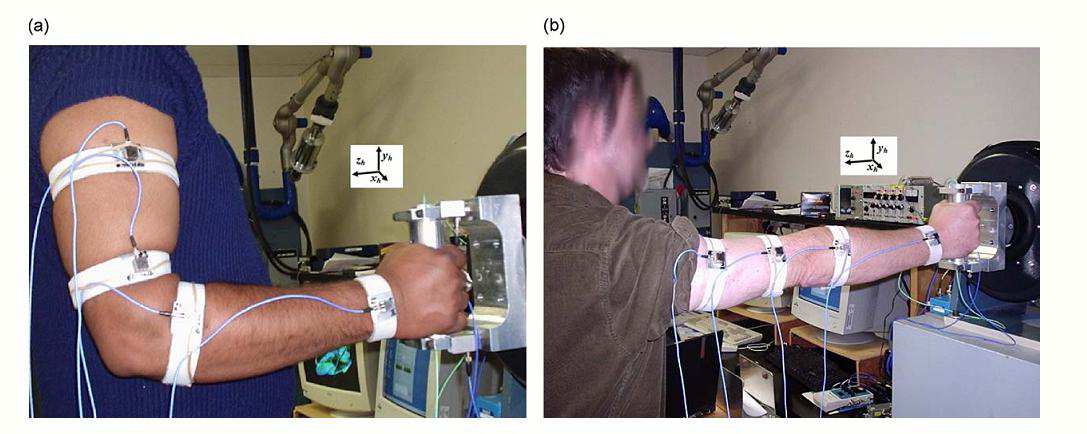
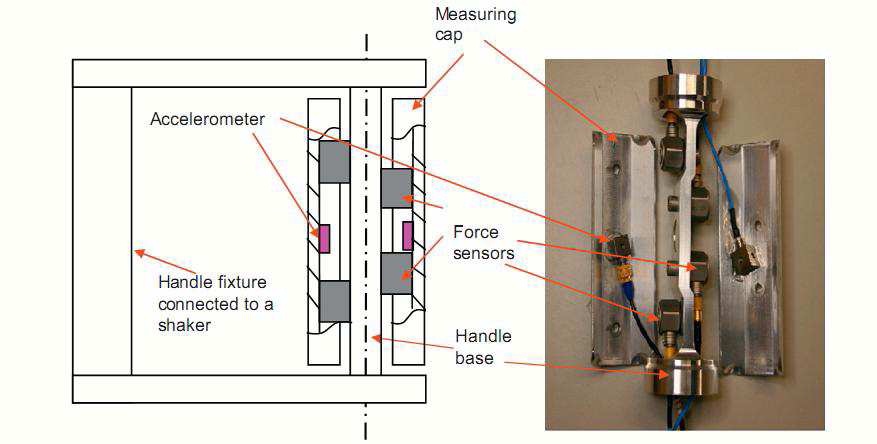
The block diagram of the experimental set-up is shown in fig 1. An instrumented 40mm diameter cylindrical handle was used in this study. The handle consists of two kistler force sensors to measure the grip force. The handle with base fixture was installed on an electrodynamic shaker. Five triaxial accelerometers were used to measure the vibration transmission. One triaxial accelerometer was installed inside the handle and other four are attached to the different locations of hand-arm system. The experiments were conducted with two different hand-arm postures (P1-bent arm with 900 elbow angle; P2- extended arm with 1800 elbow angle). The vibrations transmitted to four different locations on the hand-arm system were measured using triaxial accelerometers.
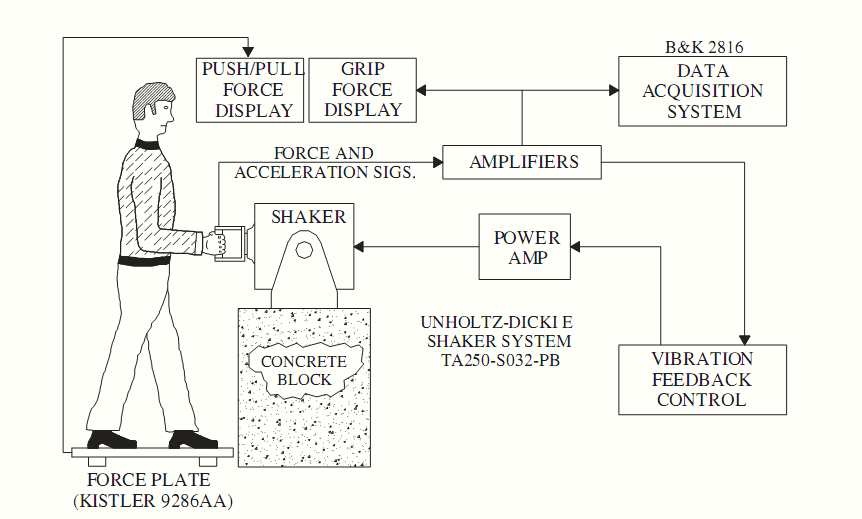
The accelerometers were attached to Velcro strips, which were tightly fastened near the joints. The locations include the wrist, shoulder and near the elbow joints on the fore arm and upper side arms. The experiments were conducted with three different grip forces (10N,30N,50N) and two different magnitudes of broad-band random vibration in the range 2.5-2500Hz. Various physical dimensions of the hand-arm system such as weight, height and body mass index are also measured, in order to study their effect on vibration transmissibility.
Mechanical equivalent model of a hand-arm system does not consider the anatomical substructures of the fingers. So it cannot be used to predict the vibration absorption power in the sections of a finger. Hence a separate modeling of the finger tip is required to analyze the vibration transmissibility. A new modeling approach known as “Vibration Power Absorption Density (VPAD)” technique is introduced to analyze the vibration exposure intensity of the soft tissues of finger tip. The technique is a hybrid modeling approach, which combines a 2D finite element (FE) model with a lumped parameter model. The lumped components are used to represent the global biodynamic characteristics of the hand-arm system whereas the FE component is used to predict the detailed stresses, strains, and VPAD in the finger tip.
The lumped parameters are determined by using the vibration transmissibility measured at the finger tip, while the material parameters of the soft and hard tissues of the FE model are adopted from the published experimental data. The proposed model was applied to predict the distributions of dynamic displacement, velocity, and VPAD in the soft tissues of the finger tip. The hybrid model of a finger tip is shown in Figure.4. The finger tip is simulated using a 2D finite element model, while the effective mass of the hand–finger is represented by the mass element m.
The coupling between the finger tip and hand–finger is represented by the spring and damping element (K1 and C1). The contact between the finger tip and the vibrating plate is simulated in the FE modeling, while the coupling between the hand and the vibrating plate is represented by a spring/damping unit (K3 and C3). The coupling between the hand, forearm, and ground is represented by using another spring/damping unit (K2 and C2). The finger tip model was assumed to be composed of skin layers, subcutaneous tissue, bone, and nail. The biquadral, plain-strain elements were used in the FE models and the commercial FE software package, ABAQUS (version 6.8), was utilized for the analyses. The nail is considered to have a thickness of 0.60mm.
The skin is assumed to be composed of two layers: the outer skin (100 mm thick) and inner skin (1.26mm thick). The outer skin layer contains stratum corneum (SC) and a part of the viable epidermis; and is considered as linearly elastic (Young’s modulus of 2MPa and Poisson’s ratio of 0.30); while the inner skin layer is composed of dermis and a part of the viable epidermis, and is characterized as nonlinearly elastic. The bone and nail are assumed to be linearly elastic, and have Poisson’s ratio of 0.30 and Young’s moduli of 17.0GPa and 170.0MPa, respectively. The vibrating plate was assumed to have a thickness of 25mm and a at contact surface. The plate was considered to be made of aluminum with Young’s modulus of 77.9GPa and Poisson’s ratio of 0.30.
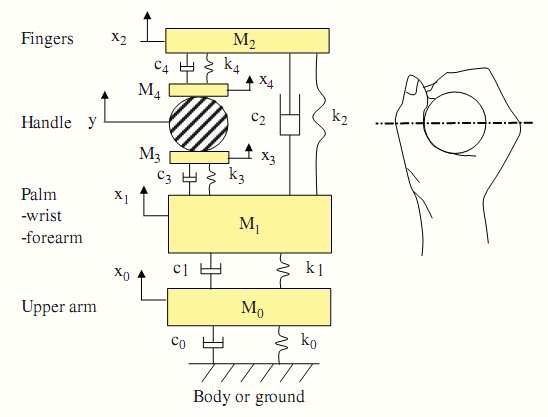
M0 is the apparent mass of shoulder and a part of the upper body. M1 is the apparent mass of palm, wrist and fore arm. M2 is the apparent mass of fingers, bones and part of the finger soft tissues. M3 is the apparent mass of palm contact skin with handle and M4 is the apparent mass of finger contact skin. K0 and C0 are the stiffness and damping coefficient of shoulder. K1 and C1 are that of forearm and K2 and C2 are of wrist and palm. Stiffness and damping coefficient of palm contact skin and finger contact skin are represented by K3, C3 and K4, C4 respectively. Y is the amplitude of excitation from the handle and x i’s are the amplitudes of vibrations of corresponding masses. The model responses were evaluated using a set of preselected model parameters and a sinusoidal input at the handle along the forearm direction at each center frequency one-third octave bands.
A new approach for assessing the transmissibility of anti-vibration gloves was proposed and evaluated in this study. A distinct advantage of this approach is that the glove transmissibility can be predicted without imposing any interference to the glove and the hand–arm system, which makes it possible to assess the true vibration isolation effectiveness of the glove. The results show that the human hand–arm system in an extended arm posture amplifies the vibration transmitted to the upper-arm and the trunk at frequencies below 25Hz. Furthermore, this posture attenuates the transmitted vibration more effectively than the bent-arm posture above 25Hz, except at the shoulder. This suggests that operators of power tools with frequencies below 25Hz may experience greater muscles/tissues fatigue and symptoms of musculoskeletal disorder when working with extended arm posture.
The results of this study demonstrate that the vibration isolation effectiveness of a glove is controlled by the resonant frequencies of the glove-hand–arm system and that reducing the resonant frequencies can increase the effectiveness of the glove. This can be achieved using two different approaches: (I) to reduce the glove contact stiffness (K5and K6) and (II) to increase the effective mass of the hand (M2 and M3). The use of the first approach can be effective for the reduction of the vibration transmitted to the palm but it is not very effective for the reduction of the vibration transmitted to the fingers. This is mainly because the finger effective mass (M2) is generally very small. The effective mass due to the fingers may also be increased by increasing the mass of the glove coupling the fingers (M8). However, it would pose design and implementation challenges, since it could raise some ergonomic problems related to dexterity loss, glove weight, and handling and control of the tool. A feasible approach is perhaps to apply a rigid metal cover on the top of an AV handle wrap, which could yield more rigid coupling (K7) between the distributed glove masses (M7 and M8).
1.John Z. Wu , Ren G. Dong, Daniel E. Welcome, Xueyan S. Xu, A method for analyzing vibration power absorption density in human fingertip,Journal of Sound and Vibration,Article in Press.
2. S.A. Adewusi, S. Rakheja, P. Marcotte, J. Boutin, Vibration transmissibility characteristics of the human hand–arm system under different postures, hand forces and excitation levels,Journal of Sound and Vibration, 329(2010) 2953-2971.
3. Ren G. Dong, Thomas W. McDowell, Daniel E. Welcome, Christopher Warrena, JohnZ. Wu, Subhash Rakheja, Analysis of anti-vibration gloves mechanism and evaluation methods, Journal of Sound and Vibration, 321(2009) 435-453.
4. R.G. Dong, D.E. Welcome, T.W. McDowell, J.Z. Wu, Measurement of biodynamic response of human hand–arm system, Journal of Sound and Vibration, 294(2006) 807-827.
| Are you interested in this topic.Then visit the below page to get the full report |