





Published on Apr 02, 2024
In electromagnetism and electronics, inductance is the property of an electrical conductor by which a change in current through it induces an electromotive force in both the conductor itself and in any nearby conductors by mutual inductance.
These effects are derived from two fundamental observations of physics: a steady current creates a steady magnetic field described by Oersted’s law, and a time-varying magnetic field induces an electromotive force (EMF) in nearby conductors, which is described by Faraday’s law of induction. According to Lenz’s law a changing electric current through a circuit that contains inductance induces a proportional voltage, which opposes the change in current (self-inductance). The varying field in this circuit may also induce an EMF in neighboring circuits (mutual inductance).
To study the factor on which the self inductance of a coil depends by observing the effect of this coil, when put in series with a resistor (bulb) in a circuit fed up by an A.C. source of adjustable frequency.
Self inductance is the property of a coil which opposes the change in current through it. The self inductance of a coil (long solenoid) is
L =( μ_0 μ_r N2 A)/l
where µr = Relative magnetic permeability of magnetic material, µr =μ/μ_0
N =Total number of turns in solenoid
A = Area of cross-section of solenoid
l = Length of solenoid
Hence, the self inductance depends upon
No. of turns in solenoid
Geometry of coil, L A , L 1/l
Nature of core material, L µ
When an inductor is connected in series with a resistor (bulb) with a variable source of frequency , then current flowing in the bulb is
Irms = E_rms/Z
where Z =√(R2 )+ ω2 L2 = Impedance of the a.c. circuit
Here R = Resistance of bulb
L = Self inductance of coil
ω = 2πf = Angular frequency of a.c. source.
The brightness of bulb i.e., Heat generated in bulb is
H = I_rme2 Zt
P = H/t = Irms2 Zt
P = Irms2 √R2 + ω2 L2
A coil of large turns, a.c. source of adjustable frequency, an electrical bulb, (6V) a.c. ammeter of suitable range rheostat, a soft iron rod, one way key, connecting wires etc.
• Make all connections as shown in circuit diagram.
• Switch on the A.C. supply and adjust the constant current in the circuit by using the variable resistor (R1) (let frequency of source is 60 Hz and voltage is 6V).
• Record the current in A.C. ammeter and see the brightness of bulb.
• Now, put the soft iron rod inside the inductor core and record the current in A.C. ammeter and again check the brightness of bulb. The current and brightness both decreases.
• Now, switch off the supply and decrease the frequency of A.C. source (say 50 Hz).
• Again switch on the supply and adjust the current in circuit at same constant voltage 6V by using the rheostat. Note the current in ammeter and brightness of bulb. The current and brightness both will increases.
• Again insert the iron in the core of coil and note the current and brightness. The current and brightness both decreases.
• Repeat the steps 5, 6 and 7 for different frequency of A.C. source(say 40 Hz,30 Hz and 20 Hz).
1. Least count of ammeter = .......... A
2. Zero error of ammeter= ............. A
3. Range of ammeter= ....................A
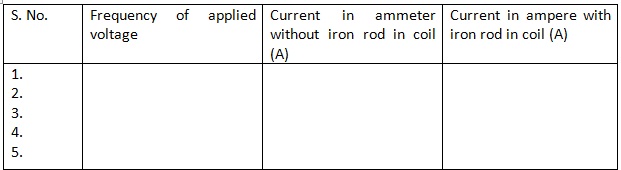
1. The current in the circuit decrease on inserting the iron rod in the core of coil at constant frequent of applied voltage and brightness of bulb decrease and vice-versa.
2. The current in the circuit increase on decreasing the frequency of applied voltage and vice-versa. Therefore, the brightness of bulb increase.
1. The coil should have number of turn.
2. Current should be passed for a small time to avoid the heating effect.
3. There should not be parallax in taking the reading of ammeter.
1. The resistance of circuit mat increase slightly due to heating effect of current.
2. There may be eddy current in soft iron coil.
In electromagnetism and electronics, inductance is the property of an electrical conductor by which a change in current through it induces an electromotive force in both the conductor itself and in any nearby conductors by mutual inductance.
These effects are derived from two fundamental observations of physics: a steady current creates a steady magnetic field described by Oersted’s law, and a time-varying magnetic field induces an electromotive force (EMF) in nearby conductors, which is described by Faraday’s law of induction. According to Lenz’s law a changing electric current through a circuit that contains inductance induces a proportional voltage, which opposes the change in current (self-inductance). The varying field in this circuit may also induce an EMF in neighboring circuits (mutual inductance).
The term inductance was coined by Oliver Heaviside in 1886. It is customary to use the symbol L for inductance, in honors of the physicist Heinrich Lenz in the SI system, the measurement unit for inductance is the Henry, with the unit symbol H, named in honor of Joseph Henry who discovered inductance independently of, but not before, Faraday.
Lenz's law named after the physicist Heinrich Lenz who formulated it in 1834, says:
The direction of current induced in a conductor by a changing magnetic field due to Faraday’s law of induction will be such that it will create a field that opposes the change that produced it.
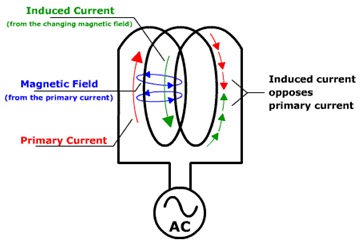
Lenz's law is shown by the negative sign in Faraday’s law of induction:-
which indicates that the induced voltage and the change in magnetic flux have opposite signs. It is a qualitative law that specifies the direction of induced current but says nothing about its magnitude. Lenz's Law explains the direction of many effects in electromagnetism, such as the direction of voltage induced in an inductor or wire loop by a changing current, or why eddy currents exert a drag force on moving objects in a magnetic field.
Lenz's law can be seen as analogous to Newton’s third law in classic mechanics.
For a rigorous mathematical treatment, see electromagnetic induction and Maxwell’s equations.
Inductors do this by generating a self-induced emf within itself as a result of their changing magnetic field. In an electrical circuit, when the emf is induced in the same circuit in which the current is changing this effect is called Self-induction, ( L ) but it is sometimes commonly called back-emf as its polarity is in the opposite direction to the applied voltage.
When the emf is induced into an adjacent component situated within the same magnetic field, the emf is said to be induced by -induction, (M) and mutual induction is the basic operating principal of transformers, motors, relays etc. Self inductance is a special case of mutual inductance, and because it is produced within a single isolated circuit we generally call self-inductance simply, Inductance.
The basic unit of measurement for inductance is called the Henry, (H) after Joseph Henry, but it also has the units of Webers per Ampere ( 1 H = 1 Wb/A ).
Lenz’s Law tells us that an induced emf generates a current in a direction which opposes the change in flux which caused the emf in the first place, the principal of action and reaction. Then we can accurately define Inductance as being: “a coil will have an inductance value of one Henry when an emf of one volt is induced in the coil were the current flowing through the said coil changes at a rate of one ampere/second”.
In other words, a coil has an inductance, ( L ) of one Henry, ( 1H ) when the current flowing through it changes at a rate of one ampere/second, ( A/s ) inducing a voltage of one volt, ( VL ) in it.
This mathematical representation of the rate of change in current through a coil per unit time is given as:
di/dt (A/s)
Where: di is the change in the current in Amperes and dt is the time taken for this current change in seconds. Then the voltage induced in a coil, ( VL ) with an inductance of L Henries as a result of this change in current is expressed as:
VL = -L di/dt (V)
Note that the negative sign indicates that voltage induced opposes the change in current through the coil per unit time (di/dt).
From the above equation, the inductance of a coil can therefore be presented as:
L = VL/(di/dt) = 1volt/(1A/s) = 1Henry
Where: L is the inductance in Henries, VL is the voltage across the coil and di/dt is the rate of change of current in Amperes per second, A/s.
Inductance, L is actually a measure of an inductors “resistance” to the change of the current flowing through the circuit and the larger is its value in Henries, the lower will be the rate of current change.
We know from the previous tutorial about the inductor, that inductors are devices that can store their energy in the form of a magnetic field. Inductors are made from individual loops of wire combined to produce a coil and if the number of loops within the coil are increased, then for the same amount of current flowing through the coil, the magnetic flux will also increase.
So by increasing the number of loops or turns within a coil, increases the coils inductance. Then the relationship between self-inductance, ( L ) and the number of turns, ( N ) and for a simple single layered coil can be given as:
L = Nφ/I
Where:
L is in Henries
N is the Number of Turns
Φ is the Magnetic Flux Linkage
Ι is in Amperes
This expression can also be defined as the flux linkage divided by the current flowing through each turn. This equation only applies to linear magnetic materials.
1. http://www.tutorvista.com/content/science/science-ii/magnetic-effects-electric-current/force-current-carrying-conductor.php
2. http://gradestack.com/CBSE-Class-10th-Course/Magnetic-Effects-of/Force-on-a-Current-/15035-2998-4742-study-wtw
3. http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/forwir2.html