





Published on Apr 02, 2024
Hooke's law is a law of physics that states that the force (F) needed to extend or compress a spring by some distance x scales linearly with respect to that distance. That is: F = kdx, where k is a constant factor characteristic of the spring: its stiffness, and x is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ut tensio, sic vis ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law already in 1660.
Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, a musician plucking a string of a guitar, and the filling of a party balloon. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean.
Hooke's law is only a first-order linear approximation to the real response of springs and other elastic bodies to applied forces. It must eventually fail once the forces exceed some limit, since no material can be compressed beyond a certain minimum size, or stretched beyond a maximum size, without some permanent deformation or change of state. Many materials will noticeably deviate from Hooke's law well before those elastic limits are reached.
In this experiment, we will study the elastic properties of a spring and of a rubber band and we will measure how closely they follow Hooke’s Law. Our present interest is in whether or not the data will fit on a linear trend line. A good fit indicates that the object (spring or rubber band) obeys Hooke’s Law. Hooke’s Law states that the restoring force is a linear function of the displacement from equilibrium.
To deform a material requires the application of a force. Some materials deform more easily than others. Materials that return to their original dimensions after the deforming force has been removed are called elastic. All materials exhibit some degree of elasticity but not always in sufficient quantity to be useful from a practical sense. The elasticity property makes its presence known through a restoring force that opposes the deformation force and tries to maintain the original dimensions of the material. We will be considering elasticity in only one dimension. The restoring force is proportional to the magnitude of the deformation. This can be expressed in an equation known as Hooke’s Law after the discoverer of the effect, Robert Hooke.
F = - kx ...................... Equation 1
The variable X represents the magnitude of the distortion or displacement from equilibrium as exhibited in the stretching of a spring or rubber band. The factor k is the proportionality constant and the minus sign indicates that the direction of the force is in the direction opposite that of the displacement, i.e. it is a restoring force.
• Computer with MS Excel
• Slotted weights
• Balance
• Coil spring
• Weight hanger
• Rod & Table
• Clamp
• Rubber band
• Meter stick
• Spring Clamp
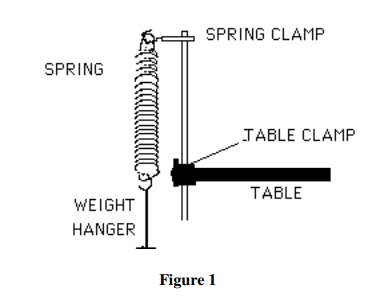
a. Mount the spring so that it hangs vertically with the small end up. Attach a 50 g mass to the hanger. This separates the coils and is your “zero” load. DO NOT COUNT THIS 50g OR THE WEIGHT HANGER AS PART OF THE “LOAD.” This is the one lab where you can neglect the mass of the weight hanger.
b. Mount the meter stick vertically in its holder with the numbers increasing towards the floor and place the meter stick on the floor. Adjust the clamp holding the spring so that the bottom of the weight hanger is sufficiently high off the ground when the heaviest load was applied. The meter stick reading that is aligned with the bottom of the weight hanger (with the 50g “zero” load) is your Reference Point – record the value below in the Data Table.
c. Now, add mass to the weight hanger, in multiples of 50 g units, until you have added 300 g. Record the meter stick reading of the bottom of the weight hanger after each mass has been added. Calculate the amount of stretch by subtracting the Reference Point value from your meter stick reading. Record this Stretch value in the Data Table below.
d. After all the masses have been added, remove them 100 grams at a time and record the meter stick readings after each change as before. This is done as a quick check on the repeatability of your data and to ensure that your Reference Point has not shifted.
a. Now, mount the rubber band in place of the spring and repeat the above experiment. Steps Ia. through Id.
• Do not stretch the rubber band with your hands before the experiment.
• Do not allow the hanger to oscillate, but hold it in position with your hand while the load is being changed.
Choose the best-fit trend line. Determine the equation of the line and its correlation coefficient. Analyze your graph.
• Does the Spring obey Hooke’s Law?.
• What characteristic of its Load vs. Stretch graph tells you this?
Choose the best-fit trend line. Determine the equation of the line and its correlation coefficient. Analyze your graph
• Does the Rubber Band obey Hooke’s Law?
• What characteristic of its Load vs. Stretch graph tells you this?
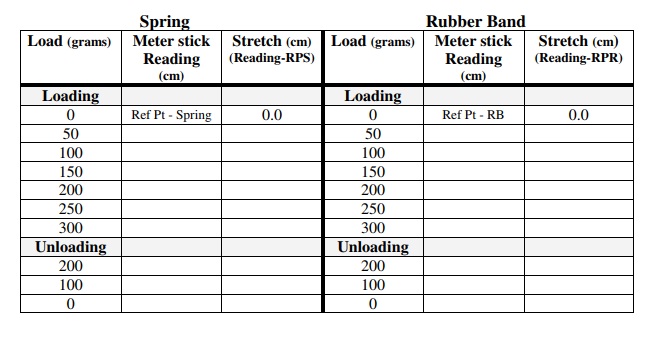
Reference Point - Spring (RPS): ___________(cm) - for “zero” load
Reference Point – Rubber Band (RPR): ___________(cm) - for “zero” load
1. http://www.tutorvista.com/content/science/science-ii/magnetic-effects-electric-current/force-current-carrying-conductor.php
2. http://gradestack.com/CBSE-Class-10th-Course/Magnetic-Effects-of/Force-on-a-Current-/15035-2998-4742-study-wtw
3. http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/forwir2.html