





Published on Apr 02, 2024
The coefficient of restitution is the ratio of the differences in velocities before and after the collision, which indicates is how much kinetic energy remains after the collision. If the coefficient of restitution is high, or close to 1, then very little kinetic energy was lost. If the coefficient is very low, or close to 0, then a large amount of kinetic energy was converted to heat or otherwise absorbed.
When a moving object, like a rubber ball, collides with an immobile surface, like a cement floor, the rubber ball will rebound with some fraction of it’s original energy. If the collision is perfectly elastic, then the ball will rebound with all of its original energy. In that case, the coefficient of restitution would be one. On the other hand, the coefficient of restitution will be close to zero then the ball will rebound with less energy then it originally arrived with if there is a permanent deformation of either the ball or the surface.
The size of the balls being used (lacrosse balls, racquetballs, and tennis balls) are part of the independent variables. Therefore, the weight of the balls could be relevant in this experiment. The lacrosse ball weighs five ounces. The racquetball weighs 1.4 ounces, and the tennis ball weighs two ounces.
The formula to calculate the coefficient of restitution is: 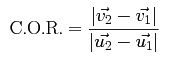
However, when the ball collides with an immobile surface the initial velocities are zero, so the formula is: Click to see the LaTeX code for this image Where v1 is the final velocity of the first object after impact, v2 is the final velocity of the second object after impact, u1 is the initial velocity of the first object before impact, and u2 is the initial velocity of the second object before impact
The purpose of this investigation is to find out the relationship of the coefficient of restitution between initial height and the height the ball bounces.
We believe that the ratio between the initial height of the ball (the independent variable) and the height the ball bounces (the dependent variable), which is defined as the coefficient of restitution, will be equal, regardless of the changes in the size of the ball and the initial height.
To being our experiment we must first gather all materials. Next, we set up the experiment in a flat part of the cul-de-sac (see diagram). To collect our data points we are going to use video analysis, so we moved camera back twenty feet from the experiment site then zoomed. Using the tape measure, we measured the first height (.5 meters). One of the group members then held the ball at measured height (.5 meters). The camera operator started the camera recording and signaled for the ball to be dropped. The person holding the ball then dropped ball from the measured height (.5 meter).
The camera recorder ended the camera recording. To make sure our data is accurate we are going to take five trials of each height, so we repeated the ball dropping from the first height for another four trials with the camera recording each trial individually. To start the next height, we measured the next height of 1 meter. The camera person then started the camera recording again and signaled for the ball to be dropped. The person holding the ball dropped the ball from the measured height (1 meter). The camera recording was then ended.
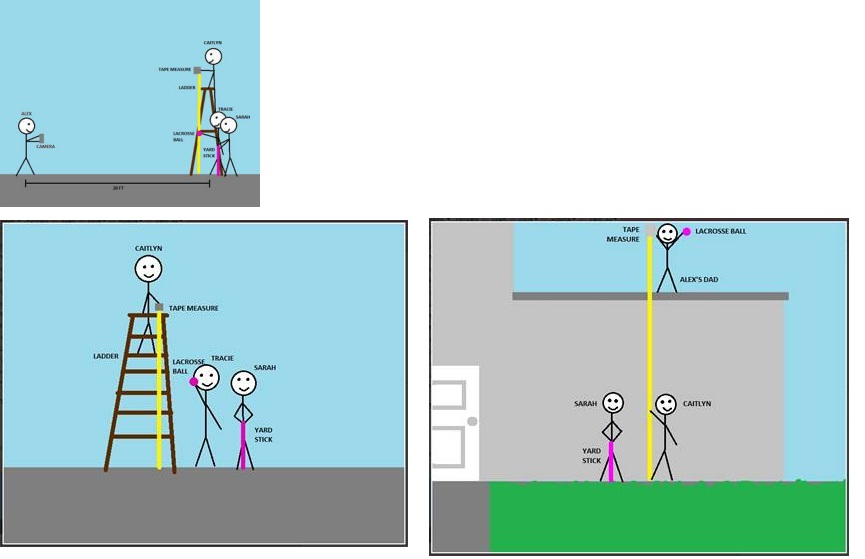
We then repeated the ball dropping from the second height for another four trials with the camera recording each trial individually to get our accurate data. We continued these steps of measuring the next height, begin recording, dropping the ball, ending the recording, and repeating for four more trials for the next seven heights (1.5 meters, 2 meters, 2.5 meters, 3 meters, 3.5 meters, 4 meters, and 4.5 meters). Once we were done with collecting the data, we uploaded all the videos to a computer and open Logger Pro. We collected the height from which the ball was dropped and the height the ball bounced to, using Logger Pro. We entered the collected data in an excel sheet. We used excel to calculate the coefficient of restitution by dividing the bounced height by the initial
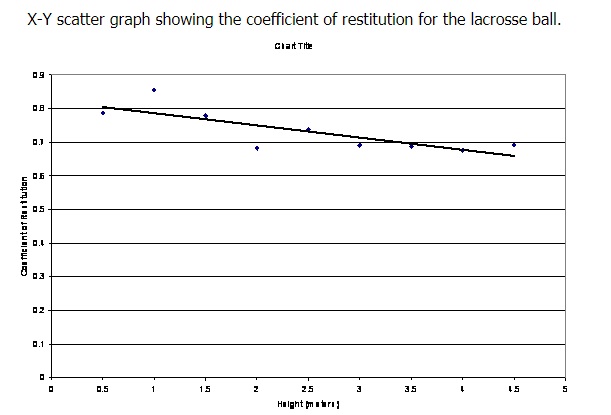
To calculate our coefficient of restitution we divided the bounced by the initial height.
Our results supported our hypothesis because the coefficient of restitution was similar for the nine heights we released the ball from. There was a slight variation in certain heights (see the conclusion for potential errors).
We believe that the ratio between the initial height and the bounced height will be equal, regardless of the change in height. Our results support our hypothesis accurately; however there are slight changes in the coefficient of restitution. The highest coefficient of restitution is .855399 and the lowest is .676307, so the difference is very small at .179092. The first source of error occurred because we had to switch locations of the experiment when we reached the maximum height of the ladder.
We transferred to the front of the house where a concert sidewalk is present, instead of the asphalt street. These two materials potentially absorb different amounts of the balls energy. Also, once we moved we had different person dropping the ball. The ball dropper on the ground and the one on the roof could have released the ball differently, therefore changing our results. Using logger pro many errors could have occurred. In logger pro each of our group members took turns using video analysis features. There we varied our collection habits.
Also, the ball in the video stretched out as it fell, so adding the points to data table and graph in logger pro was difficult because it was hard to tell exactly where to most mass of the ball was at that point. While using logger pro we uploaded the videos into the software. In some of the videos the feet were not in the frame when the ball was released which potentially messed up the origin and axes. The camera shake could have also altered our axes and origin. The yard stick we used as the constant for distance in our movie frames, if titled, would alter our height.
When the heights got taller the measuring tape tended to bend, also altering what height we released the ball from. To improve our experiment we would make sure that the surface we dropped the ball on would be the same for each drop. Also, we would put the camera on a tripod to eliminate the camera shake. We would also have the same person drop the ball each time to eliminate the variation there. The person analyzing the data on logger pro would stay the same so there are not alterations in the collection process.
1. McCutchen, Wilmot . "Coefficient of Restitution". Racquet Research. 10/23/09 <http://www.racquetresearch.com/coeffici.htm>.
2. "The Tennis Ball". International Tennis Federation. 10/23/09 <http://wings.avkids.com/Tennis/Book/ball-01.html>.
3. "Coefficient of Restitution". Physics Forums . 10/23/09 <http://www.physicsforums.com/library.php?do=view_item&itemid=270>.
4. "Coefficient of Restitution". Leader Board. 10/23/09 <http://www.leaderboard.com/GLOSSARY_COEFFICIENTOFRESTITUTION>.