





Published on Apr 02, 2024
One of the first uses of springs was in 1493, to allow an individual to shoot a pistol with only one hand. These were called non-coiled springs, which means they weren’t necessarily the windy stretchy things we know today. A spring could be made anytime a spring was tightened to allow something to bounce off of it (coiling technologies). Modern springs are known as coiled springs, and can be found anywhere from trampolines, cars, pens, toasters, and yes of course- a slinky.
A mass on a spring operates in simple harmonic motion, meaning a repetitive moving back and forth through a central point so that the maximum displacement is equal on both sides (Britannica). Because of this, moving springs can be outlined as a function of either sine or cosine. This allows us to measure things like the displacement as a function of time, period, and the number of oscillations. When you add weight to a spring, and stretch and release it, the spring begins to oscillate before it returns to its equilibrium position at rest.
Hooke’s law states that when a spring is displaced from equilibrium, it experiences a restoring force that is proportional to the displacement from equilibrium (Britannica). The formula behind is stated as: f=-kx (k is the spring constant per meter (N/m), x is the displacement (m), and f is the restoring force (N)) (Khan Academy). Engineers of machinery must know the force of a spring in order for their products to work. If a spring is too stretched or too tight, the system can be thrown out of equilibrium, causing the machine to break (More About Springs).
There are many different variables that could affect the period of the oscillation of a spring. We chose to limit our data to only manipulate the mass hanging from the spring, to more accurately determine the speed and force delivered by the spring. The same spring will have to be used in each trial to ensure accuracy of the spring constant and length of the spring. If our data does follow an exponential growth model, it may not be advisable to use masses that increase incrementally, but rather ones that would fit the model. We will determine the period as a function of the mass on the spring. To find the period T, we will use the equation T = 2π√(m/k) which relates period to mass, (M is the mass on the spring (kg), k is spring constant (N/m), and T is the period (sec)). This equation supports the idea that as the mass increases, so does the period, and that the higher the spring constant, the smaller the period. The reason for this is the greater the spring constant, the stronger the restoring force they exert is (Motion of a Mass on a Spring).
The purpose of our research is to determine the effect of mass on the period of the spring’s movement.
We predict that the period will grow in accordance with the mass. Mass is our dependent variable, measured in kilograms, and the period is our independent variable. As the masses get larger, the period should also get larger. We hope to find some correlation between the periods of the masses, which should follow an exponential decay model. Mass is defined as the measure of the mass of the weights placed on the end of the spring, and the period is the time required for the spring to complete one full cycle.
• Meter Stick
• Spring
• Mass Hanger
• Ring Stand
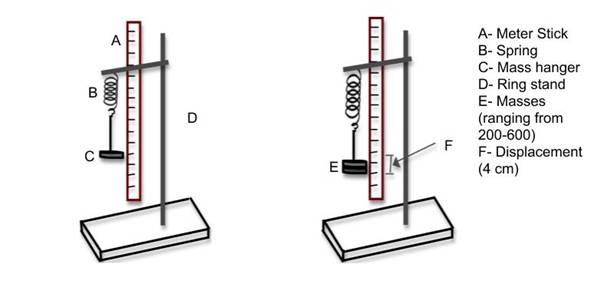
There were many different springs in the physics lab, but we chose one that had not been stretched out at all, and was still tightly coiled.
We used a ring stand at the height of 81.8 cm, with a weight hanger (50g) on one end of the spring, which hung to 41.6 cm without any additional mass added.
This will be calculated by us pulling the spring and the mass down an additional 4 cm, and letting go. We will then time the spring to see how long it takes for it to complete 10 oscillations, and then divide that time by 10, to get the period for one oscillation.
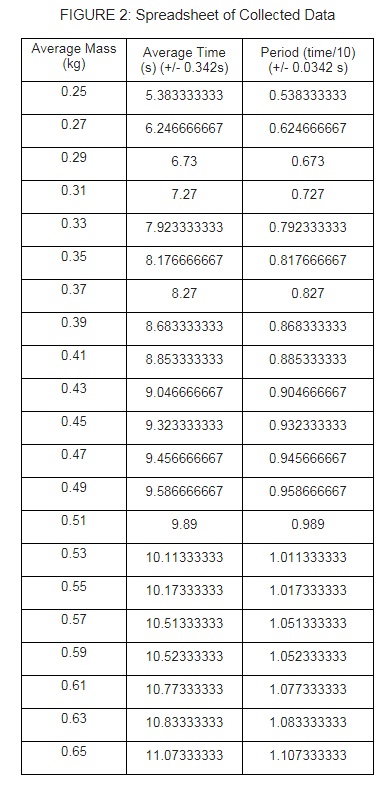
We started our mass at 200 g, and increased the mass by 20 g every time, and did three trials per mass increment. Our weight hanger was 50 g, but we accounted for that later.
We used a displacement of 4 cm. Since the displacement does not affect the period of a spring in simple harmonic motion, we picked 4 because it seemed reasonable.
The independent variable is the period of the spring. We measured this by starting a stopwatch as soon as we let go of the spring, counting 10 complete oscillations, and then stopping the stopwatch. We then divided our number by 10 to get the period for one oscillation.
The dependent variable is the mass. As stated before, we started at 200 g, and increased the mass by 20 g each time, until we reached 600 g. Our weight hanger added an additional 50 g, which we added to our values later in the experiment.
The controlled variables were; using the same spring every time, same stopwatch, and person starting/ stopping the stopwatch. Also, the same way we counted the oscillations which was, all the way stretched out to all the way coiled equaled 1, per appropriate to each mass. The starting point was also a controlled variable of ours, the spring and the weight hanger with no additional mass always started at 41.6 cm. The amount that we displaced the spring, 4 cm was also a constant of ours.
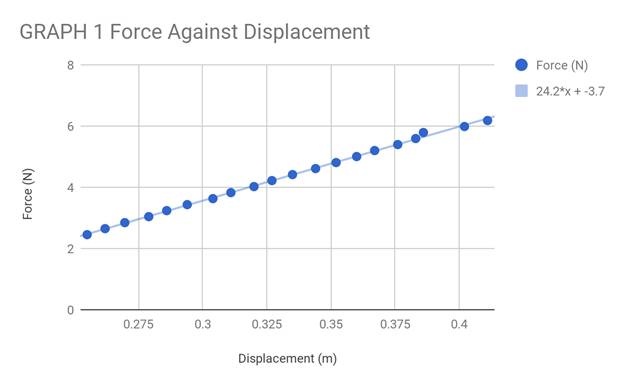
The data reveals a square root function with an equation of y = √(1.52x0.65). The data trends upwards quickly, but eventually slows and plateaus around 1.5s.
The processing of the data was all done in the spreadsheet once we programmed the formulas in.
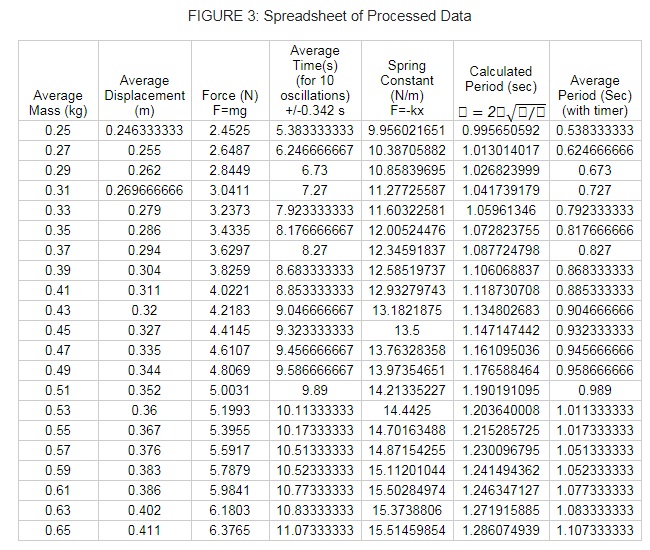
The calculated period (column 6) and the timed period (column 7) were not the same. Ideally, they would be, however due to our errors they were not. They were relatively close, and we can conclude that our data is decently reliable.
The data did overall support our hypothesis. We predicted that as the mass got larger, the period grew bigger. Our data followed a square root function, and if we had kept testing larger masses, it would have plateau somewhere between 1.5 and 2 seconds. This is due to the fact that inertia is directly related to mass. As the mass increases, so does the inertia of the system, making it harder, and slower to move. However, our data was not without error. Something that could have affected our data was that our spring had a very high spring constant; meaning that it was stiffer and more difficult to stretch. We used the equations to find the spring constant for every trial of different masses, and then we calculated the average spring constant throughout the whole experiment and got 13.494 N/m.
The tighter spring has a higher frequency making the period shorter. Additionally, our method of timing the spring was not as precise as it could be, and our calculated uncertainty of the time was +/- 0.342s. Another source of error could be while letting go of the mass, it may not have gone straight up and down, but also side to side. This was a user error, and difficult to avoid unless we had more technical equipment. Further research could find the point at which the derivative of Graph 2 gets infinitely small. This would find the point at which the period plateaus. It would also be interesting to test a wider range of masses. Due to our equipment, we were unable to do a wider range without the apparatus falling over, or the mass not moving.
1. The Editors of Encyclopedia Britannica. "Simple Harmonic Motion." Encyclopedia Britannica. Encyclopedia Britannica, Inc., 15 Feb. 2017. Web.
2. "The History of Springs." Coiling Technologies. N.p., 4 Nov. 2012. Web.
3. "More About Springs." About Springs. N.p., n.d. Web.
4. "What Is Hooke's Law?" Khan Academy. N.p., n.d. Web.
5. “Motion of a Mass on a Spring.” The Physics Classroom, www.physicsclassroom.com/class/waves/Lesson-0/Motion-of-a-Mass-on-a-Spring.