





Published on Apr 02, 2024
A slinky is a long helical spring, usually made of steel. It is flexible and has appreciable elasticity. It produces transverse waves when one end is fixed and the other end is stretched and given a jerk at right angle to its length. It produces longitudinal waves when compressions are given at regular intervals of time at the free end of the slinky. A disturbance which propagates through a medium is called wave.
In case of longitudinal waves, the particles of the medium vibrate to and fro periodically along the direction of propagation of the wave. It consists of alternate compressions and rarefactions. For example, waves along a compressed spring are longitudinal waves.
To determine the velocity of a pulse propagated through a slinky or a stretched string.
Wavelength of longitudinal waves can be defined as:
The distance covered by one complete rarefaction and one complete compression. [Or] The distance between two consecutive compressions or rarefactions.
Frequency: The number of vibrations made by a particle in the slinky per unit time (one second) is called its frequency. It is denoted by the symbol (neu).
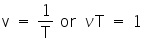
Where T is the time period which is the time taken to complete one wavelength.
When the particles of the medium periodically move up and down, perpendicular to the direction of propagation of the wave, it is called transverse wave. A transverse wave consists of alternate crests and troughs. While the wave disturbance moves in the forward direction, the medium particles show upward movement, the topmost position of displacement is known as crest. The maximum downward displacement is known as trough.

The wavelength of a transverse wave can be defined as:
Distance between two consecutive crests (C) or Distance between two consecutive troughs (T) or Distance covered by one complete crest or one complete trough (T).
Transfer waves can easily be produced along a slinky or a rope by jerking the free end up and down uniformly.
The distance travelled by the disturbance during the time period is known as wavelength ie., length of a wave. It is denoted by the symbol λ. The wavelength is equal to the distance between two consecutive crests or troughs (in case of transverse wave).
Wave Velocity or Pulse Velocity: Wave velocity is the distance travelled by the wave per second.
When the wave travels distance, λ in time T, its velocity v is equal to,

It means,
Wave Velocity = Wave Frequency X Wave Length
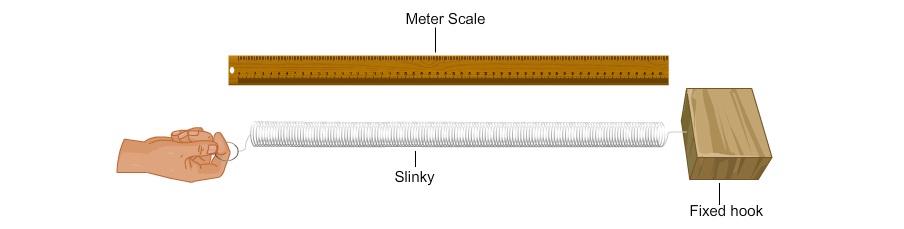
1. Take a slinky and place it lengthwise on the smooth surface of the table.
2. Tie one end of the slinky with the fixed hook.
3. Hold the free end of the slinky and stretch it (1 to 3 m depending upon the nature of slinky).
4. Move your hand periodically and uniformly at right angles to the length of the slinky.
5. Observe the propagation of the wave through the slinky and observe the formation of crests and troughs.
6. Compress the free end of the slinky periodically and observe the slinky.
Did you see an alternate compressions and rarefactions passing through the slinky?
7. Measure the wavelength by measuring the distance between two consecutive troughs (T and T) or two crests (C and C) in case of transverse wave. In case of longitudinal wave, λ is equal to distance between two consecutive compressions (C and C) or rarefactions (R and R).
8. Note the time as pulse (wave) passes through slinky for a particular distance from which we can find out the velocity of the wave.
1. On jerking the free end of a slinky at a right angle to its length, there is formation of crests and troughs, along the slinky from free end toward its fixed end.
2. When regular compressions are given at the free end of the slinky, there is movement of wave from free end towards its fixed end. The movement of the wave is associated with the formation of compression and rarefactions.
On jerking the free end of a slinky at a right angle to its length, there is formation of crests and troughs, along the slinky from free end toward its fixed end.
When regular compressions are given at the free end of the slinky, there is movement of wave from free end towards its fixed end. The movement of the wave is associated with the formation of compression and rarefactions.
1. Wavelength = the distance covered by one complete rarefaction and one complete compression.
= The distance between two consecutive crests or troughs
= ................ cm.
2. The time taken in completing one wavelength ,T =............... second.
3. The velocity of a pulse (wave) along slinky (v)
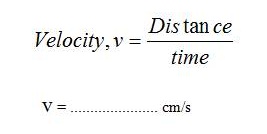

The velocity of a pulse (wave) propagated through a stretched slinky =………………..m/s
1. The slinky should have appropriate length, elasticity and flexibility.
2. One end of the slinky should be fixed properly.
3. The top of the table should be smooth.
• Manual of Secondary Science Kit for Classes IX and X - Published by NCERT
• http://epathshala.nic.in/wp-content/doc/book/flipbook/Class%20IX/0964-Science/CHAP%2012/index.html