





Published on Apr 02, 2024
Archimedes' principle states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially submerged, is equal to the weight of the fluid that the body displaces and acts in the upward direction at the center of mass of the displaced fluid. Archimedes' principle is a law of physics fundamental to fluid mechanics. It was formulated by Archimedes of Syracuse.
Practically, Archimedes' principle allows the buoyancy of an object partially or fully immersed in a fluid to be calculated. The downward force on the object is simply its weight. The upward, or buoyant, force on the object is that stated by Archimedes' principle, above. Thus, the net force on the object is the difference between the magnitudes of the buoyant force and its weight. If this net force is positive, the object rises; if negative, the object sinks; and if zero, the object is neutrally buoyant - that is, it remains in place without either rising or sinking. In simple words, Archimedes' principle states that, when a body is partially or completely immersed in a fluid, it experiences an apparent loss in weight that is equal to the weight of the fluid displaced by the immersed part of the body.
To establish the relationship between the loss in weight of a solid and weight of water displaced when the solid is fully immersed in the following solutions:
• Tap water
• Strong salty water
This can be done by using at least two different solids in the experiment.
When a metallic block is immersed in water (or any other liquid), four vertical forces act upon the block below the surface of water. These forces can be grouped into two types of forces.
1. Downward forces
a. The weight of the block.
b. The downward thrust due to pressure of the liquid on the upper surface of the block.
2. Upward forces
a. The tension of the spring, which measures the apparent weight.
b. The upward thrust due to liquid present below the lower surface of the block. This upward thrust is known as Buoyancy.
The more a body is immersed in water, the more the weight of the body decreases. The weight of the body is least when it is completely immersed in water. This means that loss in weight of the body increases as it is completely immersed in water.
Loss in weight of body = Weight of water (liquid) displaced by the body = Buoyant force or upthrust exerted by water (any liquid) on the body.
It was Archimedes who first observed that bodies lose their weight when immersed in water. He proposed a principle based on his observation that is now known as the Archimedes' Principle.
The Principle states that: “A body immersed in a liquid loses weight by an amount equal to the weight of the liquid displaced.”
Archimedes principle also states that: “When a body is immersed in a liquid, an upward thrust, equal to the weight of the liquid displaced, acts on it.”
Thus, when a solid is fully immersed in a liquid, it loses weight which is equal to the weight of the liquid it displaces.
The more the density of liquid in which the solid is immersed, the less is the weight of the liquid displaced on immersing the solid.
Some bodies, if dropped in water, sink, such as a stone or a metallic needle. On the other hand, some bodies, even of the same weight as that of those that sink, float on water. This can be proved through the Laws of Flotation.
A body will float if the weight of the body is equal to the weight of the liquid displaced.
If the weight of the immersed body is more than the weight of the water displaced, the body will sink.

We’ll first prepare the strong salty water:
Take 400 ml of tap water in a 500 ml beaker, add some common salt to it and stir well. Go on adding salt to the water and dissolve it by stirring the solution with a glass rod until some of the salt remains undissolved in the beaker. Decant the strong (saturated) salty water and store for further use.
Now to start:
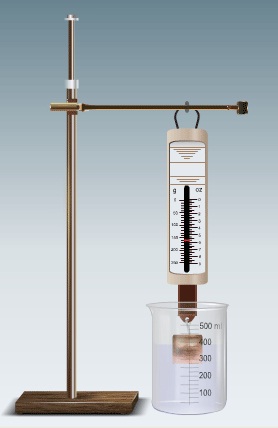
1. Hang a spring balance on an iron stand using a clamp.
2. Note the least count of the spring balance.
3. Take one of the solid blocks (S1) and weigh it by hanging it on the hook of the spring balance using a thread. Find the weight of the solid in air (Wa) and note it.
4. Take two beakers (each of 250 ml) and mark them as A and B. Weigh them on a balance separately and note down the mass of beaker A and B.
5. Take an overflow can and fill it with water to the brim of the outlet and place beaker A below the overflow outlet of the can to collect the displaced water. Now, start lowering the metallic block (S1), still attached to the spring balance into the water of the overflow can.
6. Note the loss of weight of the metallic block as it gets completely immersed in the water. Weigh beaker A which contains the displaced water and note the mass. To find the mass of the water displaced, subtract the initial mass of beaker A (without displaced water) from the present mass of the beaker A (containing displaced water).
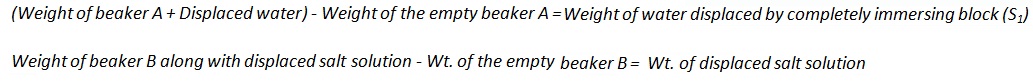
7. Repeat the experiment using the metallic block S1 by completely immersing it in the strong salty water in the overflow can. Note the loss in weight S1 by immersing it in the strong salt solution. Find the mass of the salt solution displaced and collected in the beaker.
• Weight of metallic block S1 in air = .................. g wt.
• Mass of empty beaker = ............ g.
• Weight of the block (S1) after immersed in solution = ................. g wt.
• New mass displayed in the digital balance = ................. g.
• Loss of weight of block in air = .............. g wt.
• Mass of water displaced (m) = ...................... g.
• Weight of solution displaced = m x g = ............ g wt.
5 divisions = 25 g.wt
1 division = 25/5
=5 g.wt
1. The string used to hang the spring balance should have negligible weight.
2. The metallic block should be gradually immersed in water.
3. Reading of spring balance should be taken only when it is stable.
4. When immersing the metallic block in water, care should be taken that displaced water does not spill.
• Manual of Secondary Science Kit for Classes IX and X - Published by NCERT
• DETERMINATION OF DENSITY OF LIQUIDS & SOLIDS - mhchem.org