





Published on Apr 02, 2024
During my basketball games recently, it was always my interest as to know why referees would examine the school’s basketballs. The basketballs were fully pumped, to my awareness, but the referee continued to inspect it by inserting a psi barometer into it. I remember him pushing the dial attachment and air would be released. What he was trying to measure was exactly 8.0 psi, which is the standard indoor basketball pressure. From then, I was curious as to know why basketball games have this psi regulation. What would the significance be if it were to be slightly higher- or vice versa? In what ways does a 8.0 psi benefit basketball players in general? Would the speed in which the ball bounces back from the ground increase if the psi was raised? These are the questions which motivated me to answer through this investigation.
When a basketball is inflated, it is being inserted with lots of air, similar to that of a balloon. The basic principle is that when more air is pushed into the ball, the air pressure increases because the air is being squished, trying to fit in a minimal space. As the air becomes more compact, it then pushes against itself in the ball, therefore having a force (this is called air pressure); this force is what inflates the ball into the sphere shape. When the basketball makes contact on the ground, “you are temporally pressing on the ball which squishes the air even more.”1 The importance of this is since the ball is compact with air, the air then “presses back with a certain force.”1 This certain force is the cause to the rebound of the ball; thus indicating that as higher pressures are applied, the ball will bounce higher.1 The force which the ball exerts is then followed by a velocity, and is also in the same relationship as the rebound.
Rebound, in a sports context, is when a ball bounces back from striking a hard surface or object. In this case, rebound is a significant factor, especially to those who play basketball, because it can determine the height when a basketball is dropped or dribbled on the court. However, a basketball rebound is dependent on the amounts of pressure inserted (pressure per inch). For instance, a NBA basketball psi is 8.0. This pressure is important because it provides enough rebound to NBA players, as some players are tall as 1.96 meters. However, if only 8.0 psi is enough for individuals of that height, what would happen if 7.5 psi is only inserted? Will there be a dramatic decrease in height rebound? Would the velocity be much slower when it rebounds back up? If graphed, would it be an linear growth graph?
The purpose of this investigation is to determine if different measures of PSI have a significant effect on the initial rebound height and velocity of a basketball. If a basketball, with a circumference of 75.0 centimeters, were inserted with psi’s of 4.5, 5.0, 5.5, 6.0, 6.5, 7.0, 7.5, 8.0, 8.5, 9.0, and was dropped from a height of 2.0 meters, then the psi at 9.0 would inflict a higher rebound height and velocity by 10% to the control, when compared to the psi of 4.5 which would reach 20% less than the control. This is because the extra air pressure (in psi of 8.5+) “pushes against the bottom of the ball, making it push harder against the ground.”2 Which leads to the “ground push[ing] back equally hard”2, therefore, the ball bounces back up more significantly than psi levels lower than 8.0. Brief analysis will be conducted between each sets of data tables and graphs to determine if the data outcomes stays true to the research question.
This experiment will limit to one basketball to remove any outliers and will only measure the initial rebound height. The primary focus of this investigation is the initial rebound due to basketball players constantly dribbling the ball, which eliminates the “Half-Life Theory” as part of the analysis. The force applied from the individual is a factor to be considered, but will not prevent this investigation from seeing the effects of psi on rebound height and velocity.
- Meter stick (+/-0.05cm)
- Standard Indoor Leather basketball (75 cm circumference)
- Pressure Gauge Barometer (+/- 0.05psi)
- Recording device (preferably with the slow down option)
- Ladder (optional)
An indoor basketball was utilized for the experiment. The same 75.0 centimeter circumference ball was conducted in all six trials for each psi levels. Although it is true that certain materials on the surface of the ball could result in different impacts and various forces, the standard indoor leather wrapping ball was used. The same area point on the ball was dropped as well to further reduce any possible procedural errors.
Every basketball in all psi levels were dropped from the same height of 2.0 meters. This value does not play a role in any of the calculations, but is valuable to provide a uniform height for each level.
This will be calculated from the initial bounce for each psi level. The average will be taken and it will then be inserted into a graph to determine the significance of the slope. An iphone with the slow motion option will be used to measure the height once it bounces.
The average height recorded will then be plugged into an energy conservation equation to determine the rate of the velocity applied at all psi levels. After finding the velocity, the data will be in the form of a graph to determine the significance of the slope.
The dependent variable was the basketball rebound height, h, which is measured at the maximum initial rebound in meters. To measure h, a meter stick was aligned to the wall. When the ball is dropped from the height of 2.0m and bounces back up, a phone will record the maximum height it reaches.
The independent variable are the various levels of psi: 4.5, 5.0, 5.5, 6.0, 6.5, 7.0, 7.5, 8.0, 8.5, 9.0. A higher domain would burst the basketball as basketball air pressure has a limit just like that of a balloon. A lower domain would result in no initial bounce, which would not pair well with the results.
The control variable is the standard 8.0 psi level for an indoor basketball. This psi is crucial as it will be compared to every psi above and below it to dispose the significance of the relationship between psi and height/velocity.
Controlled variables consist of: A controlled environment will be used to conduct the experiment, ensuring no wind factor, humidity, and temperature factor. Additionally, the scientific equipment will be calibrated in order to check if it is working and producing accurate outcomes with correct measurements. The basketball was dropped from the same surface at the same area. Any offset values or outliers were removed from the data collection and was redone for that trial; doing so would allow proper analysis and conclusions based on the results rather than on defective outcomes. This is a good scientific practice, demonstrating the effects of nature and procedural errors on the science at work.
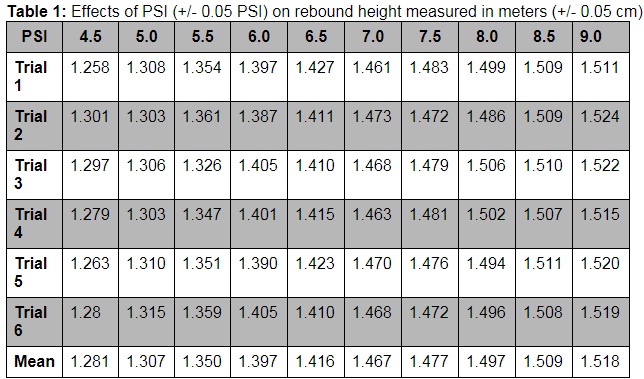
The 95% confidence interval was used to find the error bars in the graph below.
Table 2: Summarized Calculations of the effects of PSI (+/- 0.05 PSI) on rebound height measured in meters (+/- 0.05 cm).
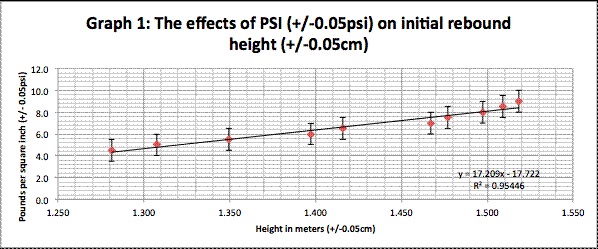
Graph 1 shows the linear growth with its equation and r2 value. This graph indicates that as the psi increases, the height in meters rises slightly, but not as significantly as predicted. As seen from the data table and the graph above, at 4.5 psi, it was at 1.281 meters. But at 9.0 psi, the height was 1.518 meters. A difference of .237 meters was shown. The r2 value is high (0.95446), indicating a low dispersion of data around the best fit line. Having this strong line suggest that the effects of psi on the initial rebound height is valid.
After acquiring the average height for each psi, it was then plugged into a conservation of energy equation to determine the rate of velocity it was moving between the ground to the air. This formula below will be used:
mgh = (1/2) mv2
m is mass, g is gravity, h is height, and v is velocity.
For example, at psi of 4.5, the calculations is as follows.
(9.81ms-2)(1.281)= (1/2)(v2)
[The mass cancels from both sides]
v(4.5) = 5.013 ms-1
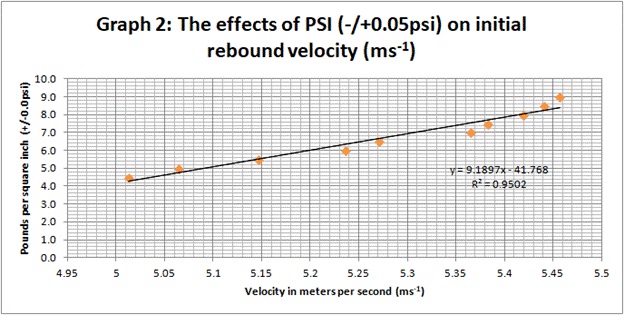
Graph 2 also indicates a linear growth in velocity. The r2 value is high (0.95015), suggesting that the dispersion of data is not far from the best fit line. This reveals how psi does have an effect on rebound velocity, but not significantly because the difference between the highest (9.0 psi) to (4.5 psi) was only .444 ms-1 apart. Error bars were not needed here because the velocity was only calculated by a formula, not recorded by the camera.
During the investigation of finding the effects of psi on rebound height and velocity, various limitations may have affected the data.
The first limitation of the data collected is the small sample size. The data only reflects 10 variations of psi and was only done for 6 trials. By not expanding more possible values, maybe as close to the maximum or slightly lower than 4.5, the data loses more available analysis.
Another limitation is the pressure gauge barometer was a manual reader. In all occasions, NBA referees and professional basketball organizations utilize a digital barometer. As a result, having a manual one and only having it read from an individual leads to human error; thus creating the large uncertainty of +/- 0.05 psi.
Identically, when the ball was performing the trials after the psi reading, some air pressure may have let loose and caused the basketball from reaching the actual height. This can be seen since some of the trial results and uncertainties are overlapping one another. To possibly fix this is to purchase a new leather indoor basketball. The one I used was a few years old and was not up to the normal conditions.
Furthermore, a limitation is that this investigation only focused on an indoor basketball. What would happen if the experiment was done on an outdoor basketball? Would the material of an outdoor basketball cause a higher significant effect on the initial rebound height and velocity?
Equally, a human error during the experiment is recording of the data. It was very difficult to actually read the maximum height of the rebound because the phone was at a slight angle. A solution to fixing this is to utilize a digital standing recording device which is capable of reading at faster frame rates. Aligning it properly would then give it the best results.
Further studies, or extensions to this, could possibly be to find the maximum height at which a indoor basketball can reach by finding the maximum pressure per inch. It is likely that the equations [ F= ma or P = F/A] be used to determine the actual pressure in the ball. Although this investigation does support that psi has an effect on rebound height and velocity, it is encouraged to try to use different types of basketball materials to test if the material is indeed a large factor towards the results.
Lastly, a limitation is that the error bars in both graphs overlap one another, suggesting that the investigation was influenced by either various factors or was a procedural error. This is most likely because of the human error of recording it based on low frame rate phone.
Overall, I was amazed that I my data could justify why an 8.0 psi is logical to be the standard pressure amount. Although the difference at 9.0 and 4.5 was not as significant as I would have thought it would be, the slight change in velocity and rebound height from these two psi levels could indeed impact a lot of players since the anticipated velocity and height would be much faster or slower. Having all basketballs regulated at 8.0 psi provides a uniform rate.s
The hypothesis was not supported. It was predicted in the hypothesis that at 9.0 psi, it would reach 10% of a greater height and velocity than the 8.0 psi (control), and at 4.5 psi, it would decrease at 20%. At 9.0 psi, the height only increased by 1.4% and the velocity by 0.7%. At 4.5 psi, it only decreased at a height by 14.4% and the velocity by 7.5%. Despite the previous mentioned limitations and unsupported hypothesis, the research question was in fact partially supported. The effects of psi on rebound height in graph 1 was not significant, but the positive linear slope suggest that the effects were prominent. Clearly, having a higher pressure does result in a larger force, supporting the methodology that psi contributes to greater rebound in both height and velocity.
1. Abel, John. “Do Basketballs That Are Fully Inflated Bounce Better than Flatter Ones?” UCSB Science Line, scienceline.ucsb.edu/getkey.php?key=3939.
2. Tamara. “Q & A: Why Do Basketballs Bounce?” Q & A: Why Do Basketballs Bounce? | Department of Physics | University of Illinois at Urbana-Champaign, van.physics.illinois.edu/qa/listing.php?id=103.