





Published on Apr 02, 2024
Aim is to find the refractive index of a) water, b) coconut oil using a plane mirror, and an equiconvex lens made of glass and an adjustable object needle.
The theory behind liquid lens is based on the properties of one or more liquids to create magnifications within a small amount of space.The focus of a liquid lens is controlled by the surface of the liquid .Water normally forms a bubble shape when adhered to materials such as glass.
This desirable property makes water a very suitable candidate for the production of liquid lens.Essentially the liquid must be transparent so as to study its effects. To generate a liquid lens , a liquid is sandwiched between two pieces of a clear plastic or a glass. Oil (necessarily transparent) can also be chosen to be used as a fluid in a liquid lens system. The surface profiles of the liquid determines the focal length of liquid lens system and how the liquid lens focusses light rays.
In optics, refractive index or index of refraction ‘n’ of a substance (optical medium) is a dimensionless number that describes how light or any radiation propagates through that medium.It is defined as
n = c/v
where’ c’ is the speed of light in vaccum and ‘v’ is the speed of light in a substance.
Eg : ‘n’ of water is 1.33, which means, light travels 1.33 times as fast in vaccum as it does in water.
The historically first occurance of refractive index was in Snell’s law of refraction.
ie are the angles of incidence of the ray crossing the interface between 2 medias with refractive indeces n_1 and n_2.
In this project, we shall make use of the property of liquid lens to find the refractive index of water and coconut oil.
A convex lens, plane mirror, water, coconut oil, an optical needle, an iron stand with base and clamp arrangement, a meter scale etc….
• Finding the focal length of convex lens:-
• Place the plane mirror with the convex lens placed on it above the horizontal base of a clamp stand horizontally as its tip lies vertically above the optic centre of the lens. Adjust the needle at a height a little more than the rough focal length of the convex lens.
• Bring the tip of the needle, at the vertical principal axis of the lens, so that the tip of the needle appears touching the tip of its image.
• Move the needle up and down to remove the parallax between tips of needle and its image.
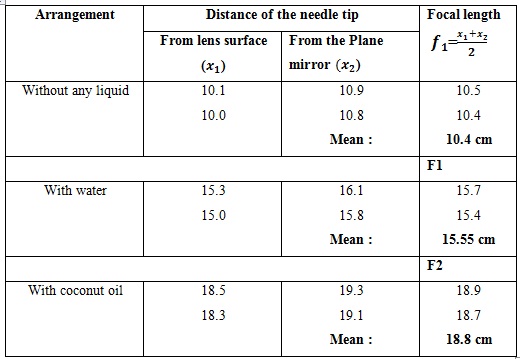
• Measure the distance between tip of the needle and upper surface of the lens by using a meter scale. Let it be (x1 ).
• Again measure the distance between tip and upper surface of the plane mirror. Let it be x2
• Finding the focal length of the combination:
• Take a few drops of the given transparent liquid and place it on the surface of plane mirror. The convex lens is placed over it as before. (A plano concave lens is formed between plane mirror and convex lens).
• Repeat the steps (ii) to (v)
• Record the observations.
• To find the radius of curvature of the liquid lens. (R of convex lens surface in contact).
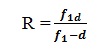
The convex lens is turned towards a source such that, the required surface is away from the source the distance is to adjusted that the image is, formed on the side of the source. The distance 'd' between the source and the lens is measured. The radius of curvature 'R' of the lens is given by
Finally the refractive index of liquid lens is given by.
n = 1+ R/f2 Result :
The observations of the experiment is tabulated as follows
• The parallax must be removed tip to tip properly.
• The lens and plane mirror should be cleaned thouroughly.
• The liquid taken should be essentially transparent.
Only few drops of liquid should be taken so that the liquid lens layer is not thick Sources of error :
• Liquid may not be quite transparent
• The parallax any not be fully removed
• The needle may not be properly horizontal
The distance x1 and x2 may not be essentially clean
The experiment described in this project is an effective and simple method of measuring the refractive index of any liquid (transparent) using a convex lens and plane mirror.
If we keep the mirror behind a lens and put an object at the focus point of the lens above it, the image of the object will form at the same focus point where the object is. If it is an extended object, its image will be inverted and the size of image is same as that of the object.
This property has enabled the efficient use of liquid lens to find the refractive index of a fluid by this method. If a liquid is sandwiched between the lens and the mirror, the focal length of liquid lens can be calculated knowing the focal length of the combination and that of the convex lens, from which the refractive index of the fluid can easily be estimated .