





Published on Apr 02, 2024
You've most likely heard the word "area" before, but you might not realize the special meaning it can have in Science and Math. In this activity you'll explore the relationship between surface area and volume. These two words are frequently heard in Nanotechnology and are important concepts to understand for many other areas of Science, too. This activity is linked to the Antibacterial Silver demonstration that you may have seen at the Small Wonders cart at a science museum.
• Learn how to calculate the surface area of cylinders
• Understand the concept of volume
• Several sheets of 8.5” x 11” paper
• A bag of popped popcorn
• A set of dry measuring cups
• Scissors
• Tape
• Pencil
• Ruler
• Calculator

• In this activity you'll be making 4 different popcorn towers using different shapes of paper folded into different ways. To start, fold one sheet of paper lengthwise (hamburger) and one piece width-wise (hotdog).
Cut along the fold for each of these pieces of paper. You should have two pairs of identical rectangles: one set long and thinner, one set shorter and wider. Label the long and skinny set T1 and T2 ("T" is for thin); label the other set W1 and W2 ("W" for wide).

• Area is the amount of space inside the boundary of a flat object, or in other terms, the size of a surface. To calculate area, measure the height and width of each piece of paper and multiply them together. Fill in the area on the chart below:

• To build the towers, roll each sheet up and tape into a tube. Make the edges of each sheet match up flush, but not overlap. Each sheet can be rolled into one of two ways: to be thin, or wide. Roll T1 so that it is a wider, short tower and T2 so that it is tall and narrow. Again, roll W1 so that it is wider and shorter and W2 so that it is taller and narrower.

• Stand each tower on end on another sheet of paper. Trace the bases of each tower so that this new sheet of paper has 4 circles on it. Label each circle so that you know to which tower (T1, T2, W1, W2) it matches.
• To calculate the total surface area, you will need to know the area of the sides of the tower (which you already found), as well as the area of the top and bottom circle. First, measure the diameter, or across the middle of each circle, and write this measurement in the table below. Also, copy the information about area from the original rectangles into this new chart.
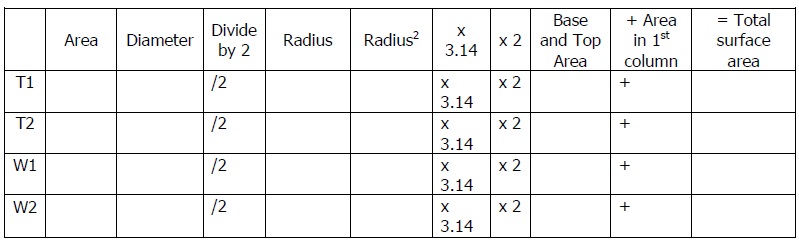
• After you find the diameter, divide by 2 to find the radius, or the distance from the center of the circle to the perimeter. Write this number in the next column.
• To find the area of a circle, you need to use the equation 3.14*Radius^2 (say: 3.14 times radius squared). To find the square, multiply the number times itself. For example, 4^2 equals 4 x 4 = 16. 5^2 equals 5 x 5 = 25.
• Calculate this number for each tower and write it in the column provided. Then multiply your "radius squared" by 3.14. Each tower has both a base and a top. You have just calculated the area of one of these circles; you must multiply this number by 2 to represent both the base and the top. Write this number in the column above.
• Finally, add the area of the sides of the tower that you calculated earlier to the number that you just wrote down. Congrats! You've found the surface area of all of your popcorn towers.
• Now we're going to explore the idea of volume. Volume is defined as the capacity or the amount of 3-dimensional space an object occupies. This is a complicated way of saying that volume is how much "stuff" fits inside a shape. It can be represented in many different units but in today's activity we're going to estimating each towers' volume in cups of popcorn!
• In the table below, write down the surface area that you calculated in the steps above, and then rank which tower you think will hold the most volume. If you think that they will all have the same volume, rank them all as "1."
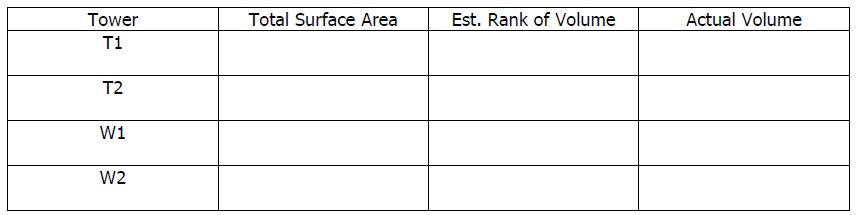
• Using the set of measuring cups, fill each paper tower with popped popcorn. Write down the volume you find in the above chart. Were your predictions correct? Can you see a relationship between container width and volume? Using a piece of paper with the same flat area as T1, T2, W1, and W2, can you make a tower with more surface area? What about a tower that holds more popcorn?

• Empty out your towers and if you’d like, eat the popcorn!
Surface area and volume are not just critical concepts to understanding why nano-silver is more effective than larger silver particles, but also an underlying theme to many other areas of nanoscience study. As particles reach the nano-scale, their large surface area to volume ratios allow for faster reactions and new chemical properties that are not always possible on the macro-scale. Through understanding the mathematical concepts and exploring how they relate to one another, you are one step closer to conducting your own nanoscience project!
1. Math is Fun! (2000). Math Definitions., retrieved May 10, 2009, from http://www.mathsisfun.com/definitions/index.html
2. Stenmark,J., Coates, G. (1986). Family Math. Berkeley, CA: Lawrence.