





Published on Jan 09, 2026
In many applications of speech processing the noise reveals some specific features. Although the noise could be quite broadband, there are a limited number of dominant frequencies, which carry the most of its energy. This fact implies the usage of narrow-band notch filters that must be adaptive in order to track the changes in noise characteristics. In present contribution, a method and a system for noise suppression are developed.
The method uses adaptive notch filters based on second-order Gray-Markel lattice structure. The main advantages of the proposed system are that it has very low computational complexity, is stable in the process of adaptation, and has a short time of adaptation. Under comparable SNR improvement, the proposed method adjusts only 3 coefficients against 250-450 for the conventional adaptive noise cancellation systems. A framework for a speech recognition system that uses the proposed method is suggested.
The noise existence is inevitable in real applications of speech processing. It is well known that the additive noise affects negatively the performance of the speech codecs designed to work with noise-free speech especially codecs based on linear prediction coefficients (LPC). Another application strongly influenced by noise is related to the hands free phones where the background noise reduces the signal to noise ratio (S/N) and the speech intelligibility.
Last but not least, is the problem of speech recognition in a noisy environment. A system that works well in noise-free conditions, usually shows considerable degradation in performance when background noise is present It is clear that a strong demand for reliable noise cancellation methods exists that efficiently separate the noise from speech signal. The endeavors in designing of such systems can be followed some 20 years ago The core of the problem is that in most situations the characteristics of the noise are not known a priori and moreover they may change in time. This implies the use of adaptive systems capable of identifying and tracking the noise characteristics. This is why the application of adaptive filtering for noise cancellation is widely used.
The classical systems for noise suppression rely on the usage of adaptive linear filtering and the application of digital filters with finite impulse response (FIR). The strong points of this approach are the simple analysis of the linear systems in the process of adaptation and the guaranteed stability of FIR structures. It is worth mentioning the existence of relatively simple and well investigated adaptive algorithms for such kind of systems as least mean squares (LMS) and recursive least squares (RLS) algorithms. The investigations in the area of noise cancellation reveal that in some applications the nonlinear filters outperform their linear counterparts. That fact is a good motivation for a shift towards the usage of nonlinear systems in noise reduction .Another approach is based on a microphone array instead of the two microphones, reference and primary, that are used in the classical noise cancellation scheme .
A brief analysis of all mentioned approaches leads to the conclusion that they try to model the noise path either by a linear or by a nonlinear system. Each of these methods has its strengths and weaknesses. For example, for the classical noise cancellation with two microphones this is the need of reference signal; for the neural filters - the fact that as a rule they are slower than classic adaptive filters and they are efficient only for noise suppression on relatively short data sequences which is not true for speech processing and finally for microphone arrays - the need of precise space alignment In present contribution the approach is slightly different.
The basic idea is that in many applications, for instance, hands-free cellular phones in car environment howling control in hands-free phones, noise reduction in an office environment, the noise reveals specific features that can be exploited. In most instances although the noise might be quite wide-band, there are always, as a rule, no more than two or three regions of its frequency spectrum that carry most of the noise energy and the removal of these dominant frequencies results in a considerable improvement of S/N ratio. This brings the idea to use notch adaptive filters capable of tracking the noise characteristics. In this paper a modification of all-pass structures is used They are recursive, and at the same time, are stable during the adaptive process. The approach is called "blind" because there is no need of a reference signal.
As mentioned in the introduction, the specific features of the noise in some speech processing applications suggest the usage of narrow-band notch filters. They have to meet the following requirements:
• To adapt as fast as possible to the changes in the noise which might be quite rapid, for example car engine noise;
• The cancelled portions of the spectrum should be as narrow as possible in order to prevent speech signal distortions.
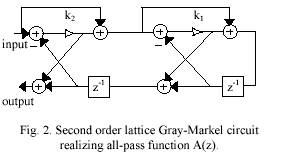
Both requirements could be met much easier using IIR adaptive filters instead of FIR adaptive filters. IIR filters are usually avoided because they create a lot of stability problems. To overcome this problem we use a realization based on second order Gray-Markel lattice circuit Fig.2. Using this circuit it becomes possible to implement a second order notch/bandpass section Fig. 3.The advantages of such a realization are first, it has extremely low pass band sensitivity that means resistance to quantization effects. Second, it is very convenient for realization of adaptive notch filters because it is possible tocontrol independently the notch frequency and the bandwidth.
The performance of the ABNS method for noise suppression is assessed by computer simulations. Fig. 5 shows the original speech. The speech is corrupted with noise from computer cooling fan that is most often encountered in office environment and the resultant signal is depicted in Fig. 6. The process of noise suppression is shown in Fig .7.
Here the system is composed of 3 sections each of them adapting its coefficient to one of the dominant frequencies in the noise spectrum. Fig.8 presents the trajectories of the filter coefficients. In this experiment the capability of the system to track the changes in noise signal is tested as the dominant frequencies shift from 0.1, 0.2 and 0.4 at the beginning, to 0.14, 0.23 and 0.36. Here the system does not have information about the dominant frequencies and adjusts its coefficients to them, as it works.
| Are you interested in this topic.Then mail to us immediately to get the full report.
email :- contactv2@gmail.com |